Introdução
Nos estudos da matemática as Funções descrevem a relação entre dois conjuntos de números através de uma lei de formação. Há uma relação entre os dois conjuntos de números, e um deles está ‘em função’ do outro. A função linear é um caso particular de função afim que apresenta a lei de formação do tipo f(x) = ax, em que a é real e diferente de zero. Por outro lado, chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0. Portanto, neste trabalho, irá falar-se da função quadrática e linear.
Função Linear E Quadrática
Definição de Função
A função determina uma relação entre os elementos de dois conjuntos. Podemos defini-la utilizando uma lei de formação, em que, para cada valor de x, temos um valor de f(x). Chamamos x de domínio e f(x) ou y de imagem da função.
A formalização matemática para a definição de função é dada por: Seja X um conjunto com elementos de x e Y um conjunto dos elementos de y, temos que: f: x → y
Assim sendo, cada elemento do conjunto x é levado a um único elemento do conjunto y. Essa ocorrência é determinada por uma lei de formação.
A partir dessa definição, é possível constatar que x é a variável independente e que y é a variável dependente. Isso porque, em toda função, para encontrar o valor de y, devemos ter inicialmente o valor de x.
Função Linear
Uma função do 1° grau ou função afim é definida pela lei de formação f(x) = a.x + b, na qual a e b são reais e a ≠ 0. Mas entre a vasta gama de funções do 1° grau, existe um tipo particular de grande importância: a função linear.
A função linear é aquela em que temos b = 0, isto é, sua lei de formação é do tipo f(x) = a.x, com a real e diferente dezero. Observe que toda função que não possui valor para o coeficiente b é classificada como função linear e, por consequência, é também uma função afim.
A função linear apresenta as seguintes características:
• a e b são números reais
• a é diferente de zero (a ≠ 0)
• b é igual a zero (b = 0)
Uma vez que b = 0, a forma da função linear é simplificada para f(x) = a.x.
Gráficos de função linear
O gráfico da função linear é representado em reta, sendo que o coeficiente linear é aquele que corta o eixo y do plano cartesiano.
Na forma matemática f(x) = a.x + b:
a = coeficiente angular (eixo x)
b = coeficiente linear (eixo y)
Exemplo 1: f(x) = 2x
Gráfico da função f(x) = 2x
Essa é uma função linear que pode ser classificada como crescente, uma vez que a = 2 > 0. Podemos visualizar seu gráfico na imagem a seguir:
Exemplo 2: f(x) = – x
2
Gráfico da função f(x) = – x/2
Essa é uma função linear decrescente, pois a = – ½ < 0. Observe seu gráfico na figura a seguir:
Exemplo 3: f(x) = 3x
Gráfico da função f(x) = 3x
Essa é uma função linear classificada como crescente, já que a = 3 > 0. Podemos visualizar seu gráfico na imagem a seguir:
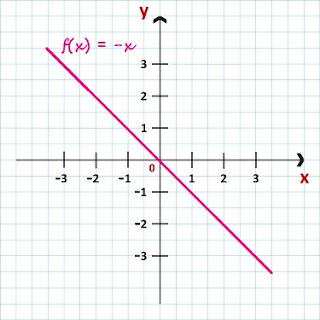
Exemplo 4: f(x) = – x
Gráfico da função f(x) = – x
Essa é uma função linear decrescente. Ela é assim classificada porque a = – 1 < 0. Veja seu gráfico:
Observe que em todos os exemplos anteriores os gráficos apresentam algo em comum. Esta é uma característica muito importante do gráfico da função linear: a reta sempre intercepta os eixos x e y na origem das coordenadas (0,0).
Exemplo 5: f(x) = x
Gráfico da função identidade - f(x) = x
Temos aqui uma função linear crescente, pois a = 1 > 0. Mas além de ser uma função linear f(x) = x, é também uma função identidade — que é do tipo f(x) = a.x, com a = 1. Veja a seguir como é o gráfico da função identidade:
O coeficiente linear é positivo quando a reta cruza o eixo y na parte positiva. O coeficiente linear, por sua vez, é negativo quando a reta cruza o eixo y na parte negativa.
Exercício Resolvido de função linear
Vamos imaginar um exemplo prático, algo que acontece diariamente nas imobiliárias.
Se a população é baixa e a grande parte das pessoas já tem a sua casa, a demanda de aluguel e venda de casas também será baixa.
Na medida em que a população aumenta, a demanda imobiliária também tende a aumentar.
Com o aumento da população, é necessário que haja mais habitações. Enquanto entre 3 e 4 milhões de habitantes, a demanda por casas é de 1 milhão, para 5 milhões de habitantes a demanda por casas aumenta para 1,5 milhão
Função quadrática ou polinomial do segundo grau
Identificamos que uma função é do segundo grau quando o maior expoente que acompanha a variável x (termo desconhecido) é 2. O gráfico da função polinomial do segundo grau sempre será uma parábola. A sua concavidade muda de acordo com o valor do coeficiente a. Sendo assim, se a é positivo, a concavidade é para cima e, se for negativo, é para baixo.
Fórmula geral da função quadrática ou polinomial do segundo grau
f(x) = ax2 + bx + c
x = domínio
f(x) = imagem
a = coeficiente que determina a concavidade da parábola.
b = coeficiente.
c = coeficiente.
Definições
Uma função definida por um polinômio do 2º grau se chama função quadrática. São exemplos de função quadrática em x:
f(x) = - 2 x2 + x + 1
g(x) = 4 x2 - 5
h(x) = x2
Definição
Uma função quadrática é uma função da forma
f(x) = a x2 + b x + c
onde a, b e c são números reais a 0.
O gráfico da função quadrática
Entre as equações quadráticas a mais simples é f(x) = x2. O seu gráfico servirá como base para construirmos os gráficos de outras equações quadráticas.
Inicialmente, apresenta-se uma simetria. Temos:
f(-2) = f(2) = 4
f(-1) = f(1) = 1
De um modo geral,
f(-x) = (-x)2 = x2 = f(x)
isto é, para todo x temos
f(-x) = f(x)
Função par
Quando uma função f satisfaz, para todo x do seu domínio, a propriedade
f(-x) = f(x)
ela se chama função par, e seu gráfico é simétrico em relação ao eixo-y
Vamos construir uma tabela com pares ordenados que são as coordenadas de pontos do gráfico da equação y = x2. Quando marcamos esses pontos em um sistema de coordenadas e os unimos em uma curva contínua, obtemos o gráfico da função f(x) = x2.
Observação:
Podemos ter uma maior precisão no gráfico marcando mais pontos. Como não podemos marcar uma infinidade de pontos, admitimos uma certa dose de confiança de que o gráfico é aquele que desenhamos.
A curva obtida se chama parábola e toda equação quadrática y = a x2 + b x + c tem uma parábola como gráfico. O domínio da função é o conjunto dos números reais e seu conjunto imagem depende dos valores de a, b e c. Para a função f(x) = x2 o conjunto imagem é constituído por todos y 0.
Uma propriedade importante dessa parábola é que ela é simétrica em relação a uma reta vertical que se chama eixo de simetria. O gráfico da equação y = x2 é simétrico em relação ao eixo-y. Essa simetria deve-se ao fato de que f(-x) = (-x)2 = x2 = f(x) e que, portanto, a função é par.
A parábola tem um ponto de retorno, que se chama vértice. O vértice é a intersecção da parábola com o eixo de simetria.
No gráfico da equação y = x2 o vértice tem coordenadas (0; 0) e o valor mínimo da função é 0.
Note que, avançando da esquerda para a direita, a curva "desce" até a origem e depois "sobe". Dizemos que f é decrescente e que f é crescente.
|
f(x) = x2 é decrescente para x 0
Se x1 < x2, então f(x1) > f(x2) |
f(x) = x2 é crescente para x 0
Se x1 < x2 , então f(x1) < f (x2) |
Função Crescente E Função Decrescente
f é crescente sobre o intervalo I se f(x1) < f(x2) sempre que x1 < x2, em I
f é decrescente sobre o intervalo I se f(x1) > f(x2) sempre que x1 < x2, em I
Exemplo
Para a função f cujo gráfico está na figura, temos:
|
intervalo
|
crescimento/decrescimento
|
|
x - 2
-2 x 2
x 2
|
f decresce
f cresce
f decresce
|
Podemos usar o gráfico da equação y = x2 para construirmos os gráficos de outras funções quadráticas. Por exemplo, os gráficos das funções y = x2 + 1 e y = x2 - 1 podem ser obtidos do gráfico da equação y = x2 por translações verticais desse gráfico.
O gráfico de y = x2 + 1 é obtido deslocando o gráfico de y = x2 + 1 unidade para cima.
O gráfico de y = x2 -1 é obtido deslocando o gráfico de y = x2 1 unidade para baixo.
Também, podemos construir os gráficos das funções y = (x - 1)2 e y = (x + 1)2 a partir do gráfico de y = x2, fazendo translações horizontais desse gráfico.
O gráfico de y = (x - 1)2 é obtido deslocando o gráfico de y = x2 1 unidade para direita. O vértice está em (1;0) e o eixo de simetria é a reta x = 1.
O gráfico de y = (x + 1)2 é obtido deslocando o gráfico de y = x2 uma unidade para a esquerda. O vértice está em (-1;0) e o eixo de simetria é a reta x = - 1.
Nos gráficos que construímos até aqui, o coeficiente de x2 é 1. Se o coeficiente é -1, o efeito sobre o gráfico é uma reflexão em relação ao eixo-x.
Então, para a função y = - x2 o domínio continua sendo o conjunto dos números reais, mas o conjunto imagem é o conjunto dos números reais y tais que y 0.
O vértice está em (0; 0) e 0 é valor máximo da função.
x
|
y = - x2
|
(x; y)
|
-3
|
-9
|
(-3; -9)
|
-2
|
-4
|
(-2; -4)
|
-1
|
-1
|
(-1; -1)
|
0
|
0
|
(0; 0)
|
1
|
-1
|
(1; -1)
|
2
|
-4
|
(2; -4)
|
3
|
-9
|
(3; -9)
|
O gráfico de y = - x2 é obtido por reflexão do gráfico de y = x2 em torno do eixo-x.
Vimos que o gráfico de y = x2 tem um ponto de retorno no vértice; ele se dobra "para cima". Dizemos que a curva tem concavidade para cima. O gráfico de y = - x2 se dobra para baixo; dizemos que a curva tem concavidade para baixo.
Quando o coeficiente a em y = a x
2 é diferente de 1, o gráfico dessa função pode ser obtido multiplicando a ordenada y, dos pontos de y = x2, pelo número a, como nos exemplos abaixo.
Cada ordenada é a metade da ordenada do gráfico de y = x2.
Cada ordenada é o dobro da ordenada do gráfico de y = x2.
Note que o gráfico de y = 2 x2 está "mais levantado" em relação ao gráfico de y = x2; o gráfico de y = 2 x2"se afasta" do eixo-x. O gráfico de y = x2 "se aproxima" do eixo-x.
Conclusão
Terminado o trabalho, pôde concluir-se que na Matemática, o conceito de função diz respeito à dependência entre duas grandezas variáveis. Cada coeficiente numérico de uma função caracteriza um elemento do gráfico dessa função. Todo gráfico de uma função do 1° grau é uma reta.
No que tange às funções quadráticas, constatou-se que o gráfico de uma função quadrática pode ou não intersectar o eixo OX, ou seja, uma função quadrática pode ter ou não zeros. É ainda importante referir que para determinar o contradomínio de uma função quadrática determinam-se as coordenadas do vértice da parábola que representa graficamente a função.
Bibliografia
• Lima, E.L.; et al. (2006). A matemática do ensino médio - vol. 1. [S.l.]: SBM
• Iezzi, G.; et al. (2013). Fundamentos de Matemática Elementar - Vol. 2 10 ed. [S.l.]: Atual.
• Stewart, James (2013). Cálculo - vol. 1 7 ed. [S.l.]: Cengage.
• Anton, H.; et al. (2014). Cálculo - Volume I 10 ed. [S.l.]: Bookman
• www.escolademoz.blogspot.com
Aulas de Moz
www.aulasdemoz.com
aulasdemoz


















Enviar um comentário
Enviar um comentário